Differentiate
Differentiate the shown equation:
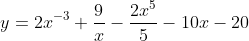
Expand Hint
The power rule for the first derivative:
$$$\frac{d}{dx}[x^n]=n\cdot x^{n-1}$$$
Hint 2
Rewriting the equation:
$$$y=2x^{-3}+9x^{-1}-\frac{2x^5}{5}-10x^{1}-20x^{0}$$$
The power rule for the first derivative:
$$$\frac{d}{dx}[x^n]=n\cdot x^{n-1}$$$
Rewriting the problem statement’s equation to be in the power rule’s format:
$$$y=2x^{-3}+9x^{-1}-\frac{2x^5}{5}-10x^{1}-20x^{0}$$$
Taking the first derivative via power rule:
$$$y'=2(-3)x^{-3-1}+(-1)9x^{-1-1}-\frac{(5)2x^{5-1}}{5}-(1)10x^{1-1}-(0)20x^{0-1}$$$
$$$y'=-6x^{-4}-9x^{-2}-2x^{4}-10x^{0}-0$$$
$$$y'=-6x^{-4}-9x^{-2}-2x^{4}-10$$$
$$$y'=-6x^{-4}-9x^{-2}-2x^{4}-10$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: The Derivative, Derivatives
048. Derivative
051. 2nd Derivatives
078. Derivatives
122. Roller Coasters
158. A Train's Velocity
312. The Derivative
394. Acceleration
412. Hill Bomb
Similar Problems from FE Section: Differential Calculus
040. Integrals
043. A Calc Question
044. Definite Integrals
048. Derivative
051. 2nd Derivatives
077. Area Under a Curve
078. Derivatives
122. Roller Coasters
158. A Train's Velocity
308. Definite Integral
312. The Derivative
342. Inflection Point
353. Inflections
355. Multi Roots
394. Acceleration
408. Triple Integrals
412. Hill Bomb
416. Trip Integral
430. A Curve’s Area
643. Integral Finding