Triple Integrals

#408 / Math Hard

Evaluate the triple integral:

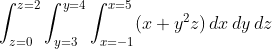
Expand Hint
Since the order of integration is specified in the problem, integrate with respect to $$x$$ first, then $$y$$ , and then finally $$z$$ .
Hint 2
$$$\int x^n \:dx=\frac{x^{n+1}}{n+1}$$$
Since the order of integration is specified in the problem, integrate with respect to $$x$$ first, then $$y$$ , and then finally $$z$$ .
$$$\int_{z=0}^{z=2}\int_{y=3}^{y=4}\int_{x=-1}^{x=5}(x+y^2z)\, dx\, dy\, dz$$$
Recall the power rule:
$$$\int x^n \:dx=\frac{x^{n+1}}{n+1}$$$
Integrate with respect to $$x$$ :
$$$=\int_{z=0}^{z=2}\int_{y=3}^{y=4}\frac{x^2}{2}+xy^2z \bigg\rvert_{x=-1}^{x=5}\, dy\, dz$$$
$$$=\int_{z=0}^{z=2}\int_{y=3}^{y=4}\frac{5^2}{2}+5y^2z-\frac{(-1)^2}{2}-(-1)y^2z \: dy\, dz$$$
$$$=\int_{z=0}^{z=2}\int_{y=3}^{y=4}12.5+5y^2z-0.5+1y^2z \: dy\, dz$$$
$$$=\int_{z=0}^{z=2}\int_{y=3}^{y=4}12+6y^2z \: dy\, dz$$$
Integrate with respect to $$y$$ :
$$$=\int_{z=0}^{z=2}12y+\frac{6y^3z}{3} \bigg\rvert_{y=3}^{y=4} \: dz$$$
$$$=\int_{z=0}^{z=2}12(4)+2(4)^3z-12(3)-2(3)^3z \: dz$$$
$$$=\int_{z=0}^{z=2}48+128z-36-54z \: dz=\int_{z=0}^{z=2}12+74z \: dz$$$
Integrate with respect to $$z$$ :
$$$=12z+\frac{74z^2}{2} \bigg\rvert_{z=0}^{z=2}=12(2)+37(2)^2-12(0)-37(0)^2 $$$
$$$=24+148-0-0=172$$$
172


☕️ Donate to keep your study guide and instructor running!
🚨 [Beta] Test your FE exam readiness with a timed quiz!
☝️ Take the survey to help us improve!

< Prev #407

random #

#409 Next >