A Curve’s Area

#430 / Math Medium

What is the area of the shaded region in the graph shown? Note the figure is not to scale.

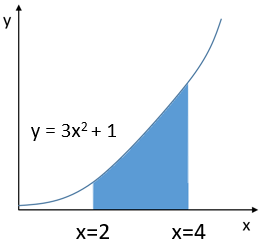
Expand Hint
Solve the definite integral of the slope while setting the lower and upper bound limits to determine the specified area under the curve.
Hint 2
The power rule:
$$$\int x^n \:dx=\frac{x^{n+1}}{n+1}$$$
Solving the definite integral of the slope while setting the upper and lower bound limits will determine the specified area under the curve.
$$$A=\int_{2}^{4}3x^{2}+1\:dx$$$
Recall the power rule:
$$$\int x^n \:dx=\frac{x^{n+1}}{n+1}$$$
Thus,
$$$A=\frac{3}{3}x^{2+1}+1x\bigg\rvert_{x=2}^{x=4}=x^{3}+x\bigg\rvert_{x=2}^{x=4}$$$
$$$=4^{3}+4-[2^{3}+2]=64+4-[8+2]=68-10=58$$$
58


☕️ Donate to keep your study guide and instructor running!
🚨 [Beta] Test your FE exam readiness with a timed quiz!
☝️ Take the survey to help us improve!

< Prev #429

random #

#431 Next >