Find the Heat Transfer and Flux
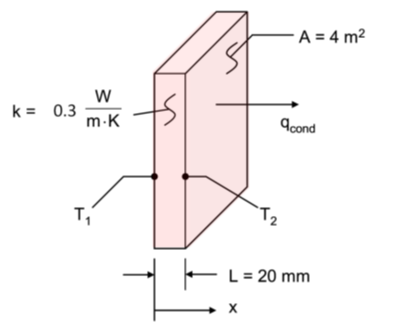
The below rectangular sheet of rigid insulation has a thermal conductivity of k = 0.3 W/m∙K, and experiences a temperature difference of T1-T2=10K across its 20-mm-thick material face sheet.
- What is the heat flux through a 2 m x 2 m sheet of the insulation?
- What is the rate of heat transfer through the sheet of insulation?
Hint
Heat flux is:
$$$q_x"=-k\frac{dT}{dx}=k\frac{T_1-T_2}{L}$$$
where
$$k$$
is the thermal conductivity,
$$dT$$
is the change in temperature, and
$$dx$$
is the distance.
Hint 2
Fourier’s Law of Conduction:
$$$q_x=q_x"\times A$$$
where
$$q_x$$
is the rate of heat transfer,
$$q_x"$$
is the heat flux, and
$$A$$
is the area.
ASSUMPTIONS
: (1) One-dimensional conduction in the x-direction, (2) Steady-state conditions, (3) Constant properties.
The heat flux equation is:
$$$q_x"=-k\frac{dT}{dx}=k\frac{T_1-T_2}{L}$$$
where
$$k$$
is the thermal conductivity,
$$dT$$
is the change in temperature, and
$$dx$$
is the distance. Solving,
$$$q_x"=0.3\frac{W}{m\cdot K}\times \frac{10K}{0.02m}=150\: \frac{W}{m^2}$$$
Fourier’s Law of Conduction:
$$$q_x=q_x"\times A$$$
where
$$q_x$$
is the rate of heat transfer,
$$q_x"$$
is the heat flux, and
$$A$$
is the area. Thus, the heat rate is:
$$$q_x=150\frac{W}{m^2}\times 4m^2=600\: W$$$
- $$150\: \frac{W}{m^2}$$
- $$600\:W$$