Piston Basics

#002 / Fluids Dynamics Medium

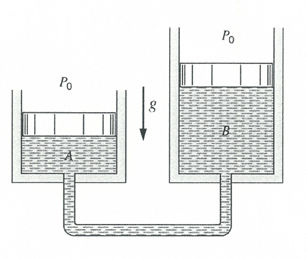
Two cylinders containing a gas are connected as shown in the figure. Piston A has a 5 cm diameter, while Piston B has a 3 cm diameter. The atmospheric pressure is 101 kPa.
  1. If the mass of Piston A is 18 kg, what is the Piston B’s mass?
  2. What is the pressure in the system?

Expand Hint
$$$Pressure=\frac{Force}{Area}=\frac{mass\times acceleration}{area}$$$
Hint 2
$$$P_0+\frac{m_Ag}{A_A}=P_0+\frac{m_Bg}{A_B}$$$
where $$P_0$$ is the atmospheric pressure, $$m$$ is the mass, $$g$$ is the acceleration due to gravity, and $$A$$ is the area.
As a system, the pressures in Piston A and Piston B are equivalent. So,
$$$P_A=P_B=\frac{Force}{Area}=\frac{mass\times acceleration}{\frac{\pi}{4}d^2}$$$
$$$P_0+\frac{m_Ag}{A_A}=P_0+\frac{m_Bg}{A_B}$$$
where $$P_0$$ is the atmospheric pressure, $$m$$ is the mass, $$g$$ is acceleration due to gravity, $$d$$ is the piston’s diameter, and $$A$$ is the area. Solving for Piston B’s mass:
$$$m_B=\frac{A_B}{A_A}m_A=\frac{\frac{\pi}{4}3^2}{\frac{\pi}{4}5^2}(18)=6.48\:kg$$$
Solving for system pressure,
$$$P_A=P_B=P_0+\frac{m_Bg}{A_B}=101+\frac{(6.48)(9.81)(10)^{-3}}{\pi (0.03)^2/4}=190\:kPa$$$
  1. 6.48 kg
  2. 190 kPa


☕️ Donate to keep your study guide and instructor running!
🚨 [Beta] Test your FE exam readiness with a timed quiz!
☝️ Take the survey to help us improve!

< Prev #001

random #

#003 Next >