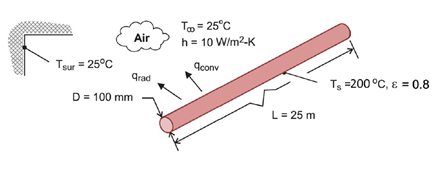
A Steam Pipe
Consider an overhead 25-m long, 100-mm diameter, uninsulated steam pipe is routed through a building whose surrounding walls and air are at 25°C, while pressurized steam maintains a pipe surface temp of 200°C. With the natural convection coefficient of h = 10 W/m^2(K), and surface emissivity of 0.8, what is the rate of heat loss from the steam line?
Hint
In this scenario, both convection and radiation are simultaneously occurring:
$$$q=q_{conv}+q_{rad}$$$
Hint 2
For radiation emitted by a body:
$$$q=\varepsilon \sigma AT^4$$$
where
$$\varepsilon$$
is the body’s emissivity,
$$\sigma$$
is the Stefan-Boltzmann constant
$$=5.67 \times 10^{-8}W/(m^2 \cdot K^4)$$
,
$$A$$
is the body’s surface area, and
$$T$$
is the absolute temperature.
ASSUMPTIONS
: (1) The steam line continuously operates throughout the year, (2) Net radiation transfer is between a small surface (steam line) and a large enclosure (plant walls).
ANALYSIS
: In this scenario, convection and radiation are both simultaneously occurring. Thus, the heat loss can be expressed as:
$$$q=q_{conv}+q_{rad}$$$
For radiation emitted by a body:
$$$q=\varepsilon \sigma AT^4$$$
where
$$\varepsilon$$
is the body’s emissivity,
$$\sigma$$
is the Stefan-Boltzmann constant
$$=5.67 \times 10^{-8}W/(m^2 \cdot K^4)$$
,
$$A$$
is the body’s surface area, and
$$T$$
is the absolute temperature.
For convection, which is the heat transfer from a heat source to a cooler object via the mass motion of a fluid, Newton’s Law of Cooling applies:
$$$q=h A(T_w-T_\infty )$$$
where
$$h$$
is the fluid’s convection heat-transfer coefficient,
$$A$$
is the convection surface area,
$$T_w$$
is the wall surface temperature, and
$$T_\infty$$
is the bulk fluid temperature.
Combining both modes of heat transfer into a single equation:
$$$q=q_{conv}+q_{rad}=A[h(T_{s}-T_\infty )+\varepsilon \sigma (T_{s}^4-T_{sur}^4)]$$$
where
$$$A=\pi DL=\pi (0.1m)(25m)=7.85m^2$$$
Finally:
$$$q=7.85m^2[10\frac{W}{m^2K}(200-25)K+0.8\cdot 5.67\times10^{-8}\frac{W}{m^2K^4}((273+200)^4-(273+25)^4)K^4]$$$
$$$q=7.85m^2[1750\frac{W}{m^2}+1912.76\frac{W}{m^2}]=28,753\:W$$$
28,753 W