Stop at the Sign
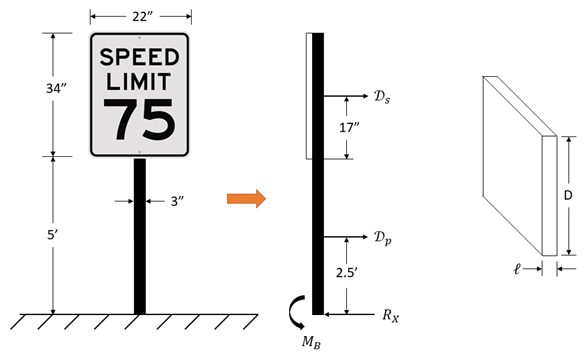
A 22 inch by 34 inch speed limit sign is supported on a 3 inch-wide, 5 ft-long pole. Estimate the bending moment in the pole at ground level when a 30 mph wind blows against the sign. Assume aspect ratio for the sign is less than 0.1. Assume the pole is a square rod with sharp corners. Also assume the density of air is 0.00238 slug/ft^3. Note the drag force coefficient of a squared rod with sharp corners is 2.2.
Expand Hint
The drag force on objects immersed in a large body of flowing fluid or objects moving through a stagnant fluid:
$$$D=\frac{1}{2}\rho U^{2}C_{D}A$$$
where
$$C_D$$
is the drag coefficient,
$$U$$
is the flowing fluid or moving object’s velocity,
$$\rho$$
is the fluid density, and
$$A$$
is the projected area of blunt objects with axes perpendicular to the flow.
Hint 2
Take the moment about the origin/base of the pole:
$$$\sum M_{o}=0=Force \times Distance$$$
For equilibrium:
$$$\sum M_{origin}=0=M_{B}-M_{P}-M_{s}$$$
where
$$M_B$$
is the bending moment,
$$M_P$$
is the moment on the pole, and
$$M_s$$
is the moment on the sign.
Remember that
$$M=Force \times Distance$$
, so the bending moment can be written as:
$$$M_{B}=2.5ft\cdot D_{P}+(5+\frac{17}{12})ft\cdot D_{s}$$$
where
$$D_P$$
is the drag force on the pole, and
$$D_s$$
is the drag force on the sign.
The drag force on objects immersed in a large body of flowing fluid or objects moving through a stagnant fluid:
$$$D=\frac{1}{2}\rho U^{2}C_{D}A$$$
where
$$C_D$$
is the drag coefficient,
$$U$$
is the flowing fluid or moving object’s velocity,
$$\rho$$
is the fluid density, and
$$A$$
is the projected area of blunt objects with axes perpendicular to the flow.
For the sign,
$$\ell/D< 0.1$$
so,
$$C_{D_s}=1.9$$
. The post acts as a squared rod with sharp corners, so
$$C_{D_p}=2.2$$
.
Thus, with
$$U=30mph=44ft/s$$
$$$D_s=\frac{1}{2}\rho U^{2}C_{D_s}A_s=\frac{1}{2}(0.00238\frac{slug}{ft^{3}})(44\frac{ft}{s})^2(1.9)(\frac{22\cdot 34}{144}ft^2)=22.7\:lb$$$
$$$D_P=\frac{1}{2}\rho U^{2}C_{D_p}A_p=\frac{1}{2}(0.00238\frac{slug}{ft^{3}})(44\frac{ft}{s})^2(2.2)(\frac{3\cdot 5}{12}ft^2)=6.34\:lb$$$
Finally,
$$$M_{B}=2.5ft\cdot (6.37lb)+(5+\frac{17}{12})ft\cdot(22.7lb)=162\:ft\cdot lb $$$
$$$162\:ft\cdot lb $$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Drag Force
021. Optimizing for Drag
362. Terminal Velocity
363. Drag Force
420. Drag Coefficient
429. Aerodynamic Drag
436. Reynolds Number Drag
442. Re Drag
462. Basketball Hoop
Similar Problems from FE Section: Consequences of Fluid Flow
021. Optimizing for Drag
362. Terminal Velocity
363. Drag Force
368. Elevated Storage Tank
420. Drag Coefficient
429. Aerodynamic Drag
436. Reynolds Number Drag
442. Re Drag
462. Basketball Hoop
Similar Problems from FE Section: Moments (Couples)
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
380. Reaction Point
499. Torque Units
656. Beam