Beam
In the simply supported beam shown, what is the vertical reaction (lb) at Point B if the downward force is 50 lb?
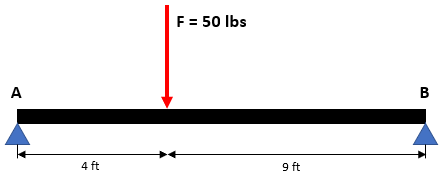
Expand Hint
Draw the free body diagram:
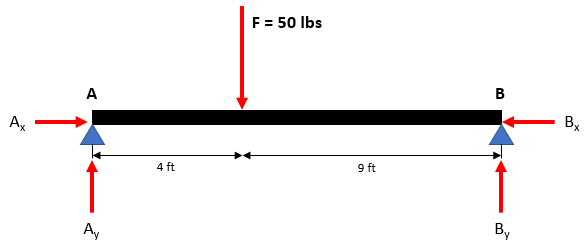
Hint 2
Take the moment about Point A to reduce the amount of unknown forces.
$$$\sum M_A=0=Force \times Distance$$$
Draw the free body diagram:
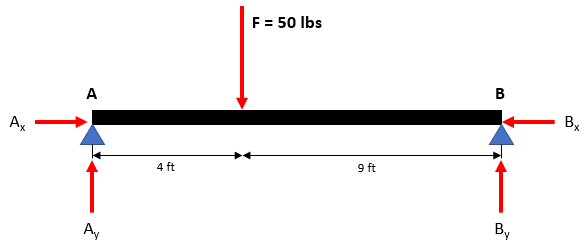
Let’s take the moment about Point A to reduce the unknown variables down to 1 (
$$A_x$$
,
$$B_x$$
and
$$A_y$$
will zero out since their radius vector goes through Point A5). Remember,
$$Moment=Force \times Distance$$
:
$$$\sum M_A=0=50lb(4ft)-B_y(4ft+9ft)$$$
$$$B_y=\frac{50lb(4ft)}{13ft}=15.4\:lb$$$
15.4 lb
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Force
055. Free Body Diagram
164. Pulleys
193. Tensional Force
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
380. Reaction Point
449. Tire Swing
Similar Problems from FE Sub Section: Moment
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
380. Reaction Point
Similar Problems from FE Section: Force
055. Free Body Diagram
145. Force Characteristics
164. Pulleys
193. Tensional Force
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
380. Reaction Point
449. Tire Swing
Similar Problems from FE Section: Moments (Couples)
047. Stop at the Sign
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
380. Reaction Point
499. Torque Units