Quadratic Equation
Find a positive value for x which satisfies the shown equation:
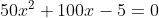
Expand Hint
Quadratic Equation Formula:
$$$x_1,x_2=\frac{-b\pm \sqrt{b^{2}-4\cdot a\cdot c}}{2a}$$$
Hint 2
Quadratic Equation Form:
$$$ax^2+bx+c=0$$$
Quadratic Equation Formula:
$$$x_1,x_2=\frac{-b\pm \sqrt{b^{2}-4\cdot a\cdot c}}{2a}$$$
Quadratic Equation Form:
$$$ax^2+bx+c=0$$$
Thus,
$$$x_1,x_2=\frac{-100\pm \sqrt{100^{2}-4\cdot 50\cdot (-5)}}{2(50)}$$$
$$$x_1,x_2=\frac{-100\pm \sqrt{10,000-(-1,000)}}{100}$$$
$$$x_1,x_2=\frac{(-100\pm 104.88)}{100}$$$
Next,
$$$x_1=\frac{(-100+ 104.88)}{100}=\frac{4.88}{100}=0.0488$$$
$$$x_2=\frac{(-100- 104.88)}{100}=\frac{-204.88}{100}=-2.0488$$$
Because
$$x_1$$
is the only positive value,
0.0488
is the answer.
0.0488
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Section: Quadratic Equation
383. Roots
560. Quad Equation
628. Imaginary Roots