Roots
Find a negative root that satisfies the shown equation:
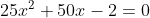
Expand Hint
Quadratic Equation Formula:
$$$x_1,x_2=\frac{-b\pm \sqrt{b^{2}-4\cdot a\cdot c}}{2a}$$$
Hint 2
Quadratic Equation Form:
$$$ax^2+bx+c=0$$$
Quadratic Equation Formula:
$$$x_1,x_2=\frac{-b\pm \sqrt{b^{2}-4\cdot a\cdot c}}{2a}$$$
Quadratic Equation Form:
$$$ax^2+bx+c=0$$$
Thus,
$$$x_1,x_2=\frac{-50\pm \sqrt{50^{2}-4\cdot 25\cdot (-2)}}{2(25)}$$$
$$$x_1,x_2=\frac{-50\pm \sqrt{2,500-(-200)}}{50}$$$
$$$x_1,x_2=\frac{(-50\pm 51.96)}{50}$$$
Next,
$$$x_1=\frac{(-50+51.96)}{50}=\frac{1.96}{50}=0.0392$$$
$$$x_2=\frac{(-50-51.96)}{50}=\frac{101.96}{50}=-2.04$$$
Because
$$x_2$$
is the only negative root,
-2.04
is the answer.
-2.04
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Section: Quadratic Equation
127. Quadratic Equation
560. Quad Equation
628. Imaginary Roots