General Forms
What shape does the shown equation represent?
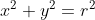
Expand Hint
The standard form of a sphere equation is:
$$$(x-h)^2+(y-k)^2+(z-m)^2=r^2$$$
where
$$r$$
is the sphere’s radius, and
$$h,k,\&\: m$$
are the respective
$$x,y,z$$
coordinates that define the sphere’s center point.
Hint 2
The standard form of a circle equation is:
$$$(x-h)^2+(y-k)^2=r^2$$$
where
$$r$$
is the circle’s radius, and
$$h\:\&\:k$$
are the respective
$$x\:\&\:y$$
coordinates that define the circle’s center point.
The standard form of a sphere equation is:
$$$(x-h)^2+(y-k)^2+(z-m)^2=r^2$$$
where
$$r$$
is the sphere’s radius, and
$$h,k,\&\: m$$
are the respective
$$x,y,z$$
coordinates that define the sphere’s center point.
The standard form of a circle equation is:
$$$(x-h)^2+(y-k)^2=r^2$$$
where
$$r$$
is the circle’s radius, and
$$h\:\&\:k$$
are the respective
$$x\:\&\:y$$
coordinates that define the circle’s center point.
If a circle were centered at the origin
$$(h=0\:\&\:k=0)$$
, then the general form is:
$$$x^2+y^2=r^2$$$
Circle
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Conic Sections
282. Conic Shapes
283. Eccentricity
284. Hyperbola
340. Zero Eccentricity
448. Ellipse
471. Greater Eccentricity
Similar Problems from FE Sub Section: Conic Section Equation
Similar Problems from FE Section: Mensuration of Areas and Volumes
282. Conic Shapes
283. Eccentricity
284. Hyperbola
340. Zero Eccentricity
448. Ellipse
471. Greater Eccentricity