Moment of Inertia
Calculate the moment of inertia of the trapezoid area about the x' axis. Assume the centroid axis line is 2.6 m away from the x-axis.
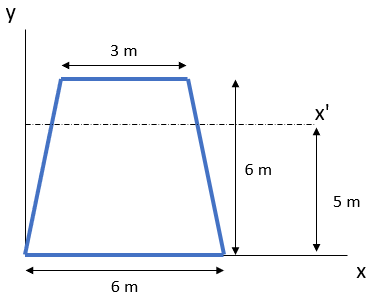
Expand Hint
Parallel Axis Theorem: The moment of inertia of an area about any axis is defined as the moment of inertia of the area about a parallel centroidal axis plus a term equal to the area multiplied by the square of the perpendicular distance
$$d$$
from the centroidal axis to the axis in question.
$$$I_{x'}=I_{xc}+d_{y}^{2}A$$$
where
$$A$$
is the area of the trapezoid:
Hint 2
First, find the moment of inertia about the centroid axis:
$$$I_{xc}=\frac{h^3(a^2+4ab+b^2)}{36(a+b)}$$$
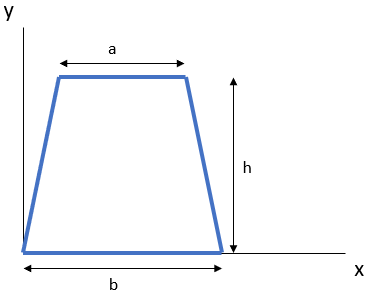
First, let's find the moment of inertia about the centroid axis:
$$$I_{xc}=\frac{h^3(a^2+4ab+b^2)}{36(a+b)}$$$
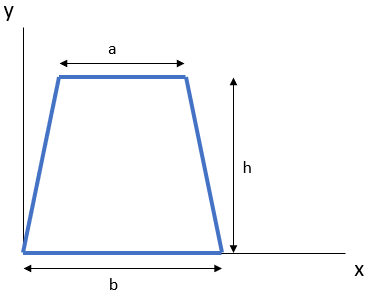
$$$I_{xc}=\frac{6^3(3^2+4(3)(6)+(6)^2)}{36(3+6)}=\frac{216(117)}{324}=78$$$
Parallel Axis Theorem: The moment of inertia of an area about any axis is defined as the moment of inertia of the area about a parallel centroidal axis plus a term equal to the area multiplied by the square of the perpendicular distance
$$d$$
from the centroidal axis to the axis in question.
$$$I_{x'}=I_{xc}+d_{y}^{2}A$$$
where
$$A$$
is the area of the trapezoid:
$$$A=\frac{h(a+b)}{2}=\frac{6(3+6)}{2}=27$$$
Finally:
$$$I_{x'}=78+(5-2.6)^{2}(27)=233.52\:m^4$$$
$$$233.52\:m^4$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Moment of Inertia Parallel Axis Theorem
229. Parallel Axis
359. Axis Theorem
Similar Problems from FE Section: Moment of Inertia
229. Parallel Axis
359. Axis Theorem