Thin Wall Cylinder
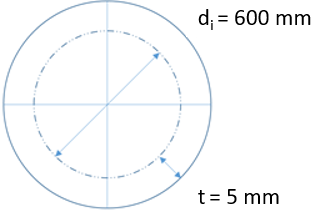
Consider an air cylinder’s pressure gauge reads 2,000 kPa. If the cylinder is made of a 5 mm steel rolled plate, with an internal diameter of 600 mm, what is the tangential stress (MPa) inside the tank?
Expand Hint
The cylinder can be considered thin-walled if:
$$$t\leq \frac{d_i}{20}$$$
where
$$t$$
is the wall thickness, and
$$d_i$$
is the inner diameter.
Hint 2
$$$\sigma_t=\frac{P_ir}{t}$$$
where
$$\sigma_t$$
is the tangential (hoop) stress,
$$P_i$$
is the internal pressure,
$$r$$
is the mean radius, and
$$t$$
is the wall thickness.
The cylinder can be considered thin-walled if
$$t\leq \frac{d_i}{20}$$
where
$$t$$
is the wall thickness, and
$$d_i$$
is the inner diameter.
$$$t\leq \frac{600mm}{20}=30\:mm$$$
Since
$$5\:mm< 30\:mm$$
, the cylinder is thin-walled.
The hoop stress formula is:
$$$\sigma_t=\frac{P_ir}{t}$$$
where
$$\sigma_t$$
is the tangential (hoop) stress,
$$P_i$$
is the internal pressure,
$$r$$
is the mean radius, and
$$t$$
is the wall thickness.
$$$r=\frac{r_{inner}+r_{outer}}{2}=\frac{(600mm/2)+[(600mm/2)+5mm]}{2}$$$
$$$=\frac{300mm+305mm}{2}=302.5mm$$$
Thus, the tangential stress is:
$$$\sigma_t=\frac{(2MPa)(302.5mm)}{5mm}=121\:MPa$$$
121 MPa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Thin-walled Cylinder
056. Tangential Stress
314. Hoop Stress
376. Pressure Cylinder
532. Axial Stress
Similar Problems from FE Section: Cylindrical Pressure Vessel
056. Tangential Stress
171. Thick Walled Vessel
314. Hoop Stress
376. Pressure Cylinder
523. Thick Vessel
528. Internal Pressure
532. Axial Stress
536. End Cap Vessel