Vertically Cantilevered
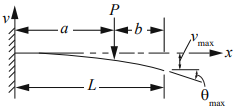
Consider a 1.25 m long solid aluminum rod with a round cross section is vertically cantilevered in the ground with a force P applied horizontally 0.1 m below the free end as shown. If there is a max deflection of 0.05 m at the rod’s free end, calculate the required force. Note the Modulus of Elasticity is 70 GPa, and the cross-sectional moment of inertia is 2.00∙10^(-8)m^4.

Expand Hint
The deflection formula for this type of cantilevered beam problem is:
$$$v_{max}=\frac{Pa^2}{6EI}(3L-a)$$$
where
$$E$$
is the Modulus of Elasticity
$$L$$
is the beam’s length,
$$P$$
is the force, and
$$I$$
is the moment of inertia.
Hint 2
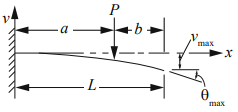
The deflection formula for this type of cantilevered beam problem is:
$$$v_{max}=\frac{Pa^2}{6EI}(3L-a)$$$
where
$$E$$
is the Modulus of Elasticity
$$L$$
is the beam’s length,
$$P$$
is the force,
$$I$$
is the moment of inertia, and
$$a$$
is:
Solving for the force,
$$P$$
:
$$$P=\frac{v_{max}(6EI)}{(3L-a)(a^2)}$$$
$$$P=\frac{(0.05m)(6)(70\cdot 10^9\frac{N}{m^2})(2\cdot 10^{-8}m^4)}{[(3)(1.25m)-(1.25m-0.1m)](1.25m-0.1m)^2}$$$
$$$=\frac{420N\cdot m^3}{(3.75m-1.15m)(1.15m)^2}=\frac{420N\cdot m^3}{(3.75m-1.15m)(1.15m)^2}$$$
$$$=\frac{420N\cdot m^3}{(2.6m)(1.323m^2)}=122.15\:N$$$
122.15 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Cantilevered Beam Slopes and Deflections
168. Cantilevered Beam
367. Superposition
Similar Problems from FE Section: Material Properties
168. Cantilevered Beam
367. Superposition