Pinball Machine
Consider you’re at an arcade, about to start a new game at the pinball machine. To launch the 0.25 kg pinball, you compress the spring 10 cm via the hand lever. After releasing the lever, the pinball launches and the game begins. What is the pinball’s velocity after travelling 5 cm if the spring’s stiffness is 25 N/m?
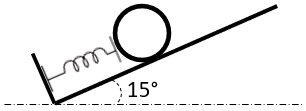
Expand Hint
Energy is not conserved:
$$$T_2+V_2=T_1+V_1+U_{1 \to 2}$$$
where
$$T$$
is the kinetic energy,
$$V$$
is the potential energy, and
$$U$$
is the work done by non-conservative forces in moving between state 1 and state 2.
Hint 2
Free body diagram of the pinball:
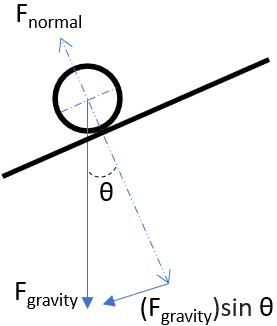
Gravity is working against the pinball (slowing it down as the ball travels upwards after release), so energy is not conserved:
$$$T_2+V_2=T_1+V_1+U_{1 \to 2}$$$
where
$$T$$
is the kinetic energy,
$$V$$
is the potential energy, and
$$U$$
is the work done by non-conservative forces in moving between state 1 and state 2. It’s important to track the algebraic sign of the work term. If the forces serve to increase the energy of the system, then work is positive. If the forces, such as friction, dissipate energy, then work is negative.
Drawing the free body diagram:
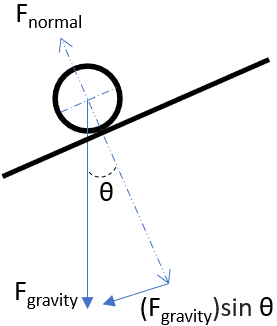
Work is negative because gravity is slowing down the pinball.
Remember, kinetic energy is:
$$$T=\frac{1}{2}mv^2$$$
where
$$m$$
is the mass and
$$v$$
is the velocity. Potential energy of a spring is:
$$$V=\frac{1}{2}ks^2$$$
where
$$k$$
is the spring constant/stiffness, and
$$s$$
is the compressed/stretched spring length. Work is:
$$$U=Force\times Distance$$$
Based on the problem statement:
- $$T_1=0$$ because the pinball is not moving so velocity is zero.
- $$V_1$$ is the potential energy of the spring being compressed prior to gameplay.
- $$V_2=0$$ because the spring is no longer compressed once released via the hand lever.
- $$T_2$$ is the kinetic energy of the pinball after the spring is released (all of the spring’s potential energy is converted to the ball’s kinetic energy minus the force of gravity).
Thus,
$$$\frac{1}{2}mv^2+0=0+\frac{1}{2}ks^2-mg\cdot sin\theta \cdot x$$$
$$$\frac{1}{2}(0.25kg)v^2=\frac{1}{2}(25\frac{N}{m})(0.1m)^2-(0.25kg)(9.8\frac{m}{s^2})\cdot sin(15^{\circ})(0.05m)$$$
$$$(0.125kg)v^2=0.125N\cdot m-0.0317N\cdot m=0.0933\:N \cdot m$$$
$$$v^2=\frac{0.0933N \cdot m}{0.125kg}=\frac{0.0933kg \cdot m^2}{0.125kg(s^2)}=0.746\frac{m^2}{s^2}$$$
$$$v=\sqrt{0.746\frac{m^2}{s^2}}=0.86\:m/s$$$
0.86 m/s
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Kinetic Energy
140. Conservation of Energy
166. Water Barrels
238. Water Barrel Collision
287. Kinetic Energy
364. Road Rash
526. K.E.
599. Formula 1 Energy
Similar Problems from FE Sub Section: Potential Energy
140. Conservation of Energy
166. Water Barrels
238. Water Barrel Collision
293. Pushing a Boulder
600. Towing a Trailer
Similar Problems from FE Sub Section: Work
364. Road Rash
Similar Problems from FE Section: Principle of Work and Energy
140. Conservation of Energy
166. Water Barrels
238. Water Barrel Collision
287. Kinetic Energy
293. Pushing a Boulder
364. Road Rash
526. K.E.
599. Formula 1 Energy
600. Towing a Trailer