Pump Efficiency
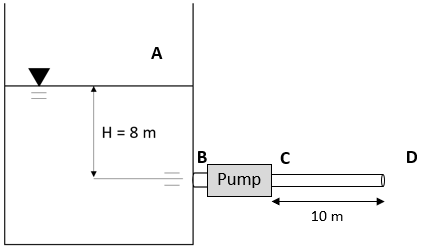
In the figure below, water is pumped through a 1 m diameter pipe from a reservoir exposed to the atmosphere (Point A). The water line is 8 m above the pipe’s centerline and the head loss due to friction is 35 m. If the motor driving the pump supplies 70 MW of power, and discharges water at 15 cubic meters per second, what is the pump’s efficiency? Note the density of water is 1,000 kg/m^3.
Expand Hint
The pump power equation:
$$$\dot{W}=\frac{Q\gamma h}{\eta_t}$$$
where
$$Q$$
is the volumetric flow,
$$h$$
is the fluid head added,
$$\eta_t$$
is the total efficiency (
$$\eta_{pump} \times \eta_{motor}$$
),
$$\dot W$$
is the power, and
$$\gamma$$
is the specific weight of the fluid.
Hint 2
The energy equation for steady incompressible flow:
$$$\frac{P_1}{\gamma }+z_1+\frac{v_1^2}{2g}=\frac{P_2}{\gamma}+z_2+\frac{v_2^2}{2g}+h_f$$$
where
$$P$$
is the pressure,
$$\gamma$$
is the specific weight,
$$z$$
is the fluid height,
$$v$$
is the velocity,
$$h_f$$
is the head loss, and
$$g$$
is the acceleration due to gravity.
First, let’s analyze the Bernoulli equation between Points A and D.
$$$H_1+H_a=H_2+H_L$$$
where
$$H_1$$
is the fluid head at Point A,
$$H_a$$
is the added fluid head,
$$H_2$$
is the fluid head at Point B, and
$$H_L$$
is the head loss. Pumps typically add energy to the system, so
$$H_a$$
is positive.
Applying the energy equation based on the problem statement:
$$$\frac{P_1}{\gamma }+z_1+\frac{v_1^2}{2g}+H_a=\frac{P_2}{\gamma}+z_2+\frac{v_2^2}{2g}+H_L$$$
where
$$P$$
is the pressure,
$$\gamma$$
is the specific weight,
$$z$$
is the fluid height,
$$v$$
is the velocity, and
$$g$$
is the acceleration due to gravity.
From the problem’s givens:
- $$P_1$$ and $$P_2$$ are atmospheric pressure, but these two terms will cancel each other.
- $$v_1=0$$ because the waterline drop at the reservoir’s surface is negligible.
- $$z_2=0$$ because we can set that as the vertical origin.
- $$z_1=8\:m$$ because Point A is 8 m higher than Point D.
- $$H_L=35\:m$$ which is the head loss from the problem statement.
- $$H_a$$ is what we are trying to determine.
- $$v_2$$ is the discharge velocity at Point D. However, we are given volumetric flow rate so we’ll need to convert.
The continuity equation:
$$$Q=Av$$$
where
$$Q$$
is the volumetric flow rate,
$$A$$
is the cross sectional area of flow, and
$$v$$
is the average fluid velocity.
Solving for velocity:
$$$v=\frac{15m^3}{\frac{\pi}{4}(1m)^2(sec)}=\frac{15}{0.785}m/s=19.11\:m/s$$$
Solving for
$$H_a$$
using the energy equation:
$$$H_a=\frac{v_2^2}{2g}+H_L-z_1$$$
$$$=\frac{(19.11m/s)^2}{2(9.8m/s^2)}+35m-8m=\frac{365.13m}{19.6}+27m$$$
$$$18.63m+27m=45.63\:m$$$
The pump power equation:
$$$\dot{W}=\frac{Q\gamma h}{\eta_t}$$$
where
$$Q$$
is the volumetric flow,
$$h$$
is the fluid head added,
$$\eta_t$$
is the total efficiency (
$$\eta_{pump} \times \eta_{motor}$$
),
$$\dot W$$
is the power, and
$$\gamma$$
is the specific weight of the fluid.
Solving for pump efficiency:
$$$\eta_t=\frac{Q\gamma h}{\dot{W}}=\frac{15m^3(9,800N)(45.63m)}{(s)(m^3)(70,000,000W)}$$$
$$$=\frac{15m^3(9,800kg\cdot m)(45.63m)(s^3)}{(s^2)(s)(m^3)(70,000,000kg \cdot m^2)}=\frac{15(9,800 )(45.63)}{(70,000,000)}=0.096$$$
The pump’s efficiency is 9.6%.
9.6%
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Pump Power Equation
182. Pump Power
213. Centrifugal Fan
297. Pressurized Pump Power
323. Pump Work
514. A Pump’s Efficiency
601. A Pump’s Pressure
Similar Problems from FE Sub Section: Energy Equation
244. Jet Velocity
Similar Problems from FE Sub Section: The Continuity Equation
178. Fluid Velocity
248. Fluid Flow
554. Fluid Density
Similar Problems from FE Section: Fluid Flow Machinery
182. Pump Power
199. Affinity Law
213. Centrifugal Fan
297. Pressurized Pump Power
323. Pump Work
348. Centrifugal Pump
474. Affinity
477. Scaling Law
514. A Pump’s Efficiency
539. Impeller Diameter
601. A Pump’s Pressure
Similar Problems from FE Section: Principles of One-Dimensional Fluid Flow
178. Fluid Velocity
248. Fluid Flow
348. Centrifugal Pump
554. Fluid Density