Ln Simplify
Simplify the shown expression:
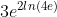
Expand Hint
The logarithm of
$$x$$
to the Base
$$b$$
is defined by
$$$log_b(x)=c$$$
where
$$b^c=x$$
.
Hint 2
Special definitions when
$$b=e$$
or
$$b=10$$
are:
- ln $$x$$ → Base = $$e$$
- log $$x$$ → Base = 10
The logarithm of
$$x$$
to the Base
$$b$$
is defined by
$$$log_b(x)=c$$$
where
$$b^c=x$$
. Special definitions when
$$b=e$$
or
$$b=10$$
are:
- ln $$x$$ → Base = $$e$$
- log $$x$$ → Base = 10
According to log properties, the
$$2$$
coefficient in front of the natural log can be rewritten as the exponent raised by the quantity inside the log.
$$$3e^{2ln(4e)}=3e^{ln[(4e)^2]}$$$
Since the natural log has a base of
$$e$$
, raising the log by base
$$e$$
will eliminate both the
$$e$$
and natural log:
$$$3e^{ln[(4e)^2]}=3(4e)^2$$$
Thus,
$$$3(4e)^2=3\times 16e^2=48e^2$$$
$$$48e^2$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Section: Logarithms
434. Logarithm
461. Log
465. Base Log
468. Ln Base
470. Natural Log
603. Bearing Type
604. Variable e
630. Type of Bearing