Tensile and Compression Tests
What theory is based upon the results of tensile and compression tests?
Expand Hint
A tensile test is a way to determine how much force is needed to break or change the shape of a material when it is being pulled apart. On the other hand, a compression test measures the amount of force needed to change the shape or compress a material when it is being pushed together. Both the tensile and compression tests help determine important material characteristics such as its tensile strength, yield strength, and elasticity.
Hint 2
The theory is used to calculate the failure load of a brittle material.
A tensile test is a way to determine how much force is needed to break or change the shape of a material when it is being pulled apart. On the other hand, a compression test measures the amount of force needed to change the shape or compress a material when it is being pushed together. Both tests help determine important material characteristics such as its tensile strength, yield strength, and elasticity.
The Coulomb-Mohr theory uses results from the tensile and compression tests to determine failure for brittle materials. On the
$$\sigma$$
and
$$\tau$$
coordinate system shown in the figure, one dotted circle is plotted for tensile strength (
$$S_{ut}$$
), and the other dotted circle for compressive strength (
$$S_{uc}$$
). Lines are then drawn tangent to these circles to form a min/max envelope. The Coulomb-Mohr theory states that failure will occur whenever a stress situation produces a circle that is either tangent to or crosses the envelope defined by the
$$S_{ut}$$
and
$$S_{uc}$$
circles.
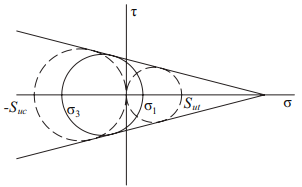
When
$$\sigma_1\geq \sigma_2 \geq \sigma_3$$
and
$$\sigma_3<0$$
, then the theory predicts yielding will occur whenever:
$$$\frac{\sigma_1}{S_{ut}}-\frac{\sigma_3}{S_{uc}}\geq 1$$$
Coulomb-Mohr
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Brittle Materials
Similar Problems from FE Section: Static Loading Failure Theories
274. Max Shear Stress Theory
522. Material Yielding