Resistance
In the below resistor circuit diagram, what is the equivalent resistance at terminals A-B?
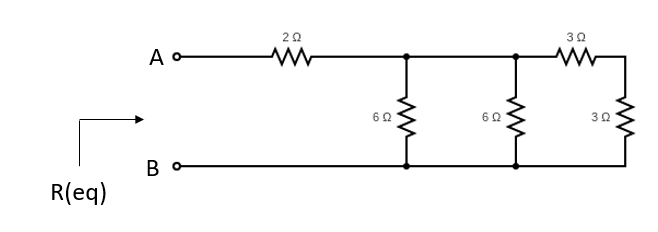
Expand Hint
For resistors in Parallel:
$$$\frac{1}{R_{T}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}...+\frac{1}{R_{n}}$$$
Hint 2
For resistors in Series:
$$$R_{T}=R_{1}+R_{2}+R_{3}...+R_{n}$$$
The problem statement is asking to find the total resistance in the circuit, which has certain sections both in series and in parallel.
The equivalent resistance for
$$n$$
resistors in Parallel:
$$$\frac{1}{R_{T}}=\frac{1}{R_{1}}+\frac{1}{R_{2}}+\frac{1}{R_{3}}...+\frac{1}{R_{n}}$$$
The equivalent resistance for
$$n$$
resistors in Series:
$$$R_{T}=R_{1}+R_{2}+R_{3}...+R_{n}$$$
Breaking down the diagram into smaller portions, let’s analyze the the highlighted section first.
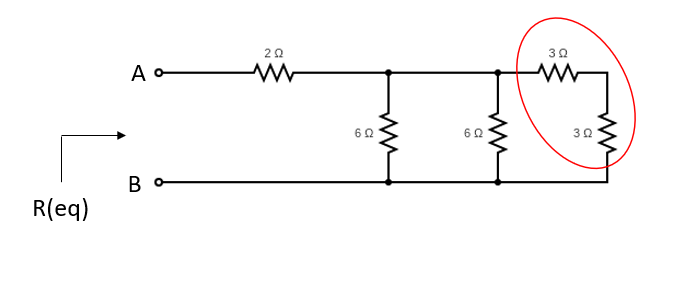
These two resistors are in series, so
$$R_T=3+3=6\Omega$$
. The diagram can now be redrawn as:
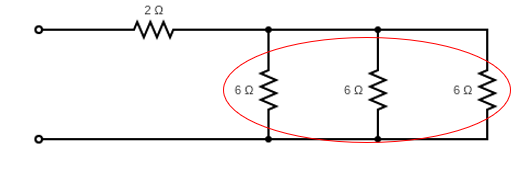
These three resistors are in parallel, so
$$R_{T}=\frac{1}{\frac{1}{6}+\frac{1}{6}+\frac{1}{6}}=2\Omega$$
, so the redrawn diagram:
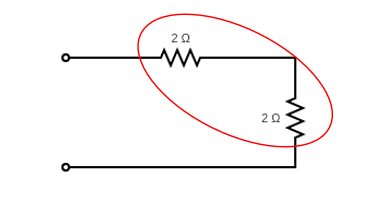
Finally, the simplified diagram of the original problem are two resistors in series, meaning the equivalent resistance at Terminals A-B is
$$R_T=2+2=4\:\Omega$$
.
4 Ω
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Resistors in Series and Parallel
069. A Capacitor's Voltage
181. Resistors in Parallel
185. Resistors in Series
490. Total Resistance
568. Total Resist
Similar Problems from FE Section: Electrostatics
010. Electric Vehicle Basics
066. Powering a Motor
069. A Capacitor's Voltage
099. Kirchhoff's Laws
116. Power
134. Hot Pot
181. Resistors in Parallel
184. Current Flow
185. Resistors in Series
291. Heating Element
439. Toaster Oven Resistor
490. Total Resistance
510. Current
512. Voltage
521. Custom PC
549. Circuit Diagram
550. Conductor Resistance
568. Total Resist
569. Parallel Plates
644. Kirchhoff’s 2nd Law