Axis Theorem
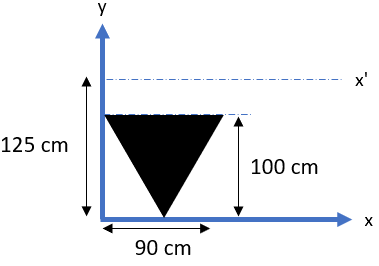
In the figure below, what is the moment of inertia about the x’ axis in m^4?
Expand Hint
Parallel Axis Theorem:
$$$I_x=I_{x_{c}}+d_{y}^{2}A$$$
where
$$d_y$$
is the distance between the new axis and the object’s centroid,
$$I_{x_{c}}$$
is the moment of inertia about the centroid axis,
$$A$$
is the total cross sectional area, and
$$I_x$$
is the moment of inertia about the new axis.
Hint 2
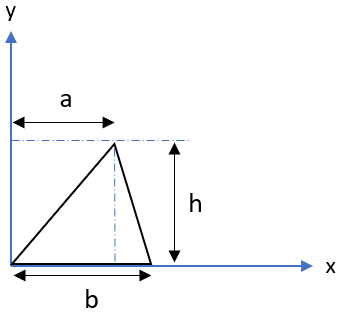
The moment of inertia about the centroid axis of a triangle:
$$$I_{x_{c}}=\frac{bh^3}{36}$$$
where
$$b$$
and
$$h$$
are defined as:
Parallel Axis Theorem:
$$$I_x=I_{x_{c}}+d_{y}^{2}A$$$
where
$$d_y$$
is the distance between the new axis and the object’s centroid,
$$I_{x_{c}}$$
is the moment of inertia about the centroid axis,
$$A$$
is the total cross sectional area, and
$$I_x$$
is the moment of inertia about the new axis.
Most online tables (including the FE handbook) for area moment of inertia and centroids will have a figure similar to this:
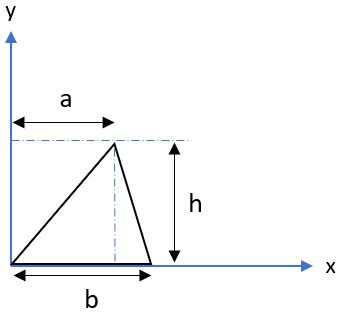
where the centroid and moment of inertia about the centroid axis are respectively defined as:
$$$y_c=\frac{h}{3}$$$
$$$I_{x_{c}}=\frac{bh^3}{36}$$$
Keep in mind that the problem is not identical to the reference figure (it’s flipped vertical). Therefore, the triangle’s centroid relative to the x-axis is actually:
$$$y_c=\frac{2h}{3}=\frac{2(1m)}{3}=\frac{2m}{3}=0.667\:m$$$
Since
$$d_y$$
is the distance between the new axis and the object’s centroid:
$$$d_y=x'-y_c=1.25m-0.667m=0.5833\:m$$$
Fortunately, the moment of inertia about the centroid axis equation remains the same:
$$$I_{x_{c}}=\frac{(0.9m)(1m)^3}{36}=\frac{0.9m^4}{36}=0.025\:m^4$$$
Thus, the moment of inertia about the x’ axis is:
$$$I_x=0.025m^4+(0.5833m)^2[\frac{1}{2}(0.9m)(1m)]=0.025m^4+0.34m^2(\frac{0.9m^2}{2})$$$
$$$=0.025m^4+0.153m^4=0.18\:m^4$$$
$$$0.18\:m^4$$$
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Moment of Inertia Parallel Axis Theorem
196. Moment of Inertia
229. Parallel Axis
Similar Problems from FE Section: Moment of Inertia
196. Moment of Inertia
229. Parallel Axis