Cosine Law
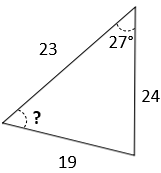
For the triangle figure shown, what is the unknown angle in degrees?
Expand Hint
Law of Cosines:
$$$a^2=b^2+c^2-2bc\:cos\:A$$$
Hint 2
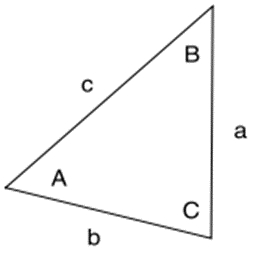
For oblique (non-right) triangles, use the Law of Cosines to determine unknown sides/angles:
$$$a^2=b^2+c^2-2bc\:cos\:A$$$
$$$b^2=a^2+c^2-2ac\:cos\:B$$$
$$$c^2=a^2+b^2-2ab\:cos\:C$$$

Thus, to find angle
$$A$$
:
$$$a^2=b^2+c^2-2bc\:cos\:A$$$
$$$2(19)(23)\:cos\:A=(19)^2+(23)^2-(24)^2$$$
$$$(874)\:cos\:A=361+529-576=314$$$
$$$cos\:A=\frac{314}{874}\Rightarrow B=cos^{-1}\left ( \frac{314}{874} \right )$$$
$$$B=cos^{-1}(0.359)=68.9^{\circ}$$$
68.9°
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Law of Cosines
346. Law of Cosines
390. Cosines
529. Unknown Side
Similar Problems from FE Section: Trigonometry
346. Law of Cosines
390. Cosines
393. Law of Sines
529. Unknown Side
533. Sines
537. Sin