Piston Basics
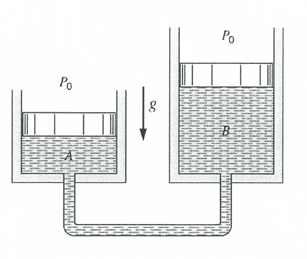
Two cylinders containing a gas are connected as shown in the figure. Piston A has a 5 cm diameter, while Piston B has a 3 cm diameter. The atmospheric pressure is 101 kPa.
- If the mass of Piston A is 18 kg, what is the Piston B’s mass?
- What is the pressure in the system?
Expand Hint
$$$Pressure=\frac{Force}{Area}=\frac{mass\times acceleration}{area}$$$
Hint 2
$$$P_0+\frac{m_Ag}{A_A}=P_0+\frac{m_Bg}{A_B}$$$
where
$$P_0$$
is the atmospheric pressure,
$$m$$
is the mass,
$$g$$
is the acceleration due to gravity, and
$$A$$
is the area.
As a system, the pressures in Piston A and Piston B are equivalent. So,
$$$P_A=P_B=\frac{Force}{Area}=\frac{mass\times acceleration}{\frac{\pi}{4}d^2}$$$
$$$P_0+\frac{m_Ag}{A_A}=P_0+\frac{m_Bg}{A_B}$$$
where
$$P_0$$
is the atmospheric pressure,
$$m$$
is the mass,
$$g$$
is acceleration due to gravity,
$$d$$
is the piston’s diameter, and
$$A$$
is the area. Solving for Piston B’s mass:
$$$m_B=\frac{A_B}{A_A}m_A=\frac{\frac{\pi}{4}3^2}{\frac{\pi}{4}5^2}(18)=6.48\:kg$$$
Solving for system pressure,
$$$P_A=P_B=P_0+\frac{m_Bg}{A_B}=101+\frac{(6.48)(9.81)(10)^{-3}}{\pi (0.03)^2/4}=190\:kPa$$$
- 6.48 kg
- 190 kPa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Stress, Pressure, and Viscosity
032. Viscosity Variations
074. Dynamic Viscosity
235. Kinematic Viscosity
446. Viscous Density
527. S.G.
530. Spec Weight
534. SW
Similar Problems from FE Section: Definitions
004. Stress and Strain
007. Aluminum Alloy Graphs
032. Viscosity Variations
074. Dynamic Viscosity
084. Specific Gravity
174. Elongation
202. Uniaxial Loading
214. Steam Engine Piston
231. Subway Hand Rail
235. Kinematic Viscosity
275. Unpressurized Vessel
309. Strain
317. Utility Pole
332. Bulk Modulus of Elasticity
349. Compressibility Modulus
350. Poisson’s Ratio
374. Test Specimen
403. Train Tracks
446. Viscous Density
451. Poisson
452. Test Coupon
453. Shear Stress & Strain
460. Shear Modulus
463. Newtonian Fluid
467. Bulk vs Shear Modulus
469. Flow Characterization
479. Piston Loading
527. S.G.
530. Spec Weight
534. SW
573. Hooke’s Law
580. Modulus of Elasticity
648. Elongating
Similar Problems from FE Section: Particle Kinetics
030. Newton's 2nd Law
488. Block Speed