How does CPU Cooling Work?
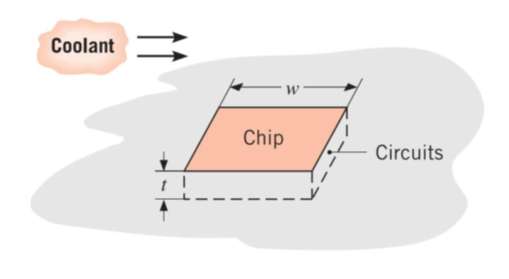
A square silicon chip (k = 150 W/m∙K) is of width w = 5 mm on a side and of thickness t = 1 mm. The chip is mounted in a substrate such that its side and back surfaces are insulated, while the front surface is exposed to a coolant. If 40 W are being dissipated in circuits mounted to the back surface of the chip, what is the steady-state temperature difference between back and front surfaces?
Hint
Fourier's law of conduction:
$$$\dot{Q}=kA\frac{\Delta T}{dx}$$$
where
$$\dot{Q}$$
is the rate of heat transfer,
$$k$$
is the thermal conductivity,
$$A$$
is the surface area perpendicular to the direction of heat transfer,
$$\Delta T$$
is the change in temperature, and
$$dx$$
is the distance.
Hint 2
$$$\Delta T=\frac{t\times \dot{Q}}{k\cdot w^2}$$$
ASSUMPTIONS
: (1) Steady state conditions, (2) Constant properties, (3) Uniform heat dissipation, (4) Negligible heat loss from back and sides, (5) One-dimensional conduction chip.
All the electrical power dissipated at the chip’s back surface is transferred by conduction. From Fourier’s law:
$$$\dot{Q}=kA\frac{\Delta T}{dx}$$$
where
$$\dot{Q}$$
is the rate of heat transfer,
$$k$$
is the thermal conductivity,
$$A$$
is the surface area perpendicular to the direction of heat transfer,
$$\Delta T$$
is the change in temperature, and
$$dx$$
is the distance. Thus,
$$$\Delta T=\frac{t\times \dot{Q}}{k\cdot w^2}=\frac{0.001m\times 40W}{150W/m\cdot K(0.005m)^2}=11\:K$$$
11 K