In-plane Shear Stress
In the element shown, what is the max in-plane shear stress in MPa?
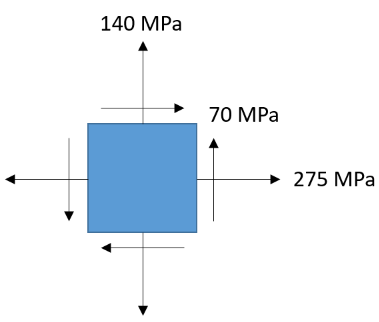
Expand Hint
Mohr's Circle:
$$$R=\sqrt{(\frac{\sigma _{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}$$$
Hint 2
$$\sigma_x$$
,
$$\sigma_y$$
, and
$$\tau_{xy}$$
are defined as:
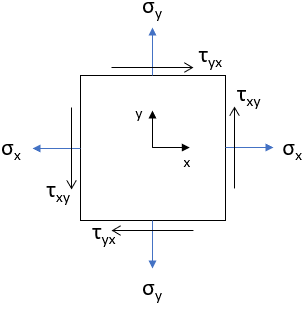
From a constructed Mohr's Circle, the max in-plane shear stress occurs when
$$\tau_{max}=R$$
$$$R=\sqrt{(\frac{\sigma _{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}$$$
Thus, the max in-plane shear stress is:
$$$R=\sqrt{(\frac{275-140}{2})^{2}+70^{2}}$$$
$$$R=\sqrt{4,556.25+4,900}=97.24\:MPa$$$
97.24 MPa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Mohr's Circle – Stress, 2D
559. Mohr’s Circle
Similar Problems from FE Sub Section: Principal Stresses
170. Principal Stress
559. Mohr’s Circle
Similar Problems from FE Section: Stress and Strain
170. Principal Stress
275. Unpressurized Vessel
559. Mohr’s Circle
573. Hooke’s Law