Principal Stress
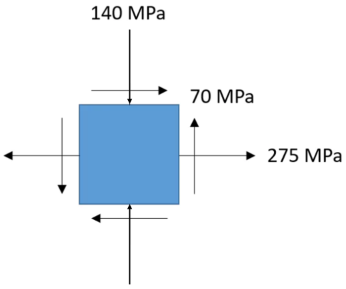
In the element shown, calculate the max tensile principal stress in MPa.
Expand Hint
For the special case of a two-dimensional stress state, the equation for principal stress reduces to:
$$$\sigma _a,\sigma _b=\frac{\sigma_x+\sigma_y}{2}\pm \sqrt{(\frac{\sigma _{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}$$$
Hint 2

For the special case of a two-dimensional stress state, the equation for principal stress reduces to:
$$$\sigma _a,\sigma _b=\frac{\sigma_x+\sigma_y}{2}\pm \sqrt{(\frac{\sigma _{x}-\sigma_{y}}{2})^{2}+\tau_{xy}^{2}}$$$
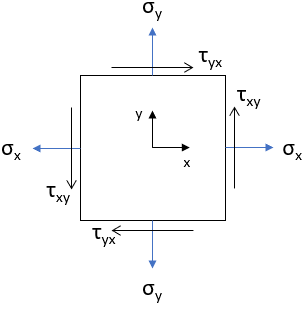
Comparing the problem's figure to the above equation format,
$$\sigma_y$$
is -140 MPa due to the downward direction the arrow is pointed in. Thus,
$$$\sigma _a,\sigma _b=\frac{275+-140}{2}\pm \sqrt{(\frac{275-(-140)}{2})^{2}+70^{2}}$$$
$$$\sigma _a,\sigma _b=67.5\pm \sqrt{43,056.25+4,900}=67.5\pm219$$$
$$$\sigma _a=67.5+219=286.5\:MPa$$$
$$$\sigma _b=67.5-219=-151.5\:MPa$$$
The max principal stress is 286.5 MPa.
286.5 MPa
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Principal Stresses
070. In-plane Shear Stress
559. Mohr’s Circle
Similar Problems from FE Section: Stress and Strain
070. In-plane Shear Stress
275. Unpressurized Vessel
559. Mohr’s Circle
573. Hooke’s Law