A Beam
Beam AB, which is simply supported at Points A & B, is subjected to a distributed load as shown. If the beam’s weight is negligible, what is the reaction force at Point B?
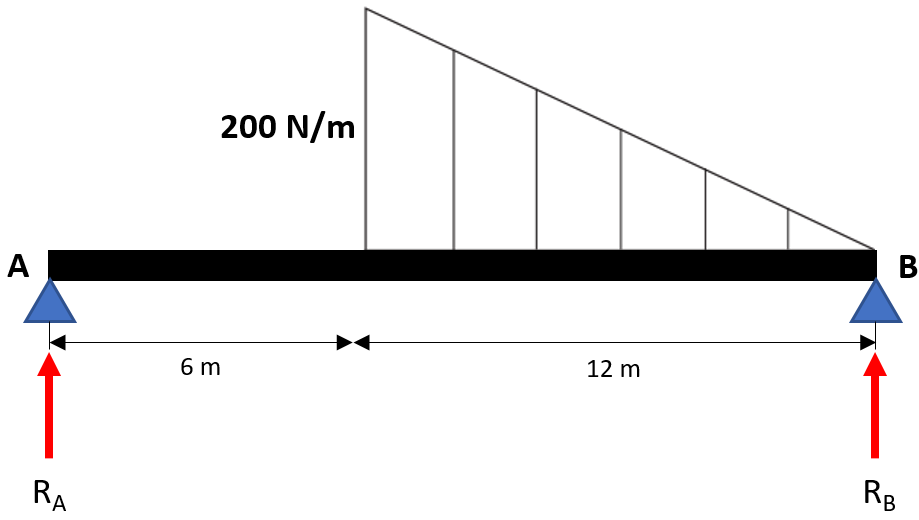
Expand Hint
Draw the free body diagram:
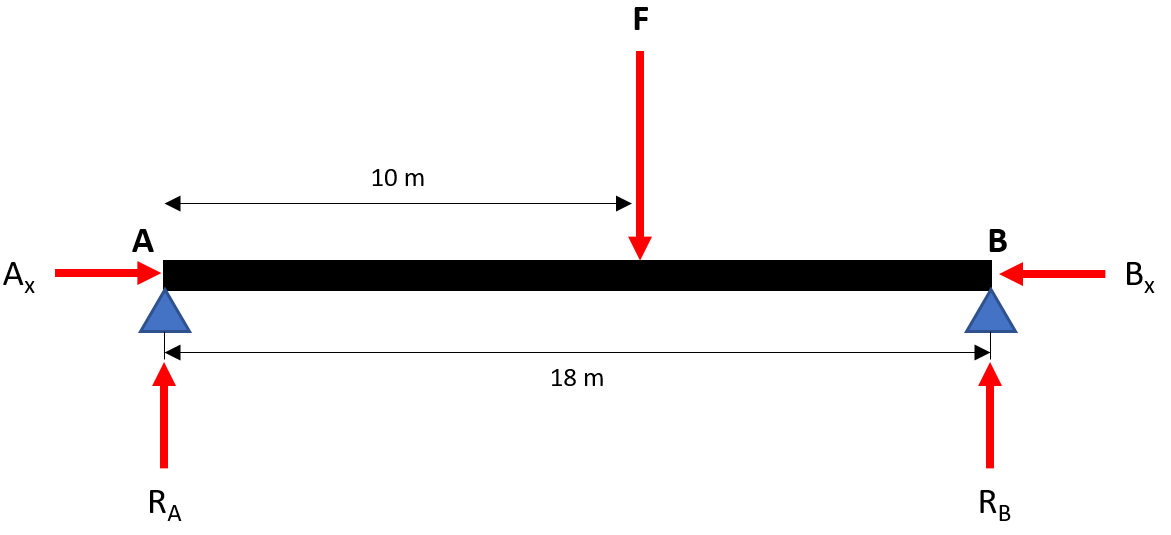
Hint 2
Take the moment about Point A to reduce the amount of unknown forces.
$$$\sum M_A=0=Force \times Distance$$$
First, draw the free body diagram:
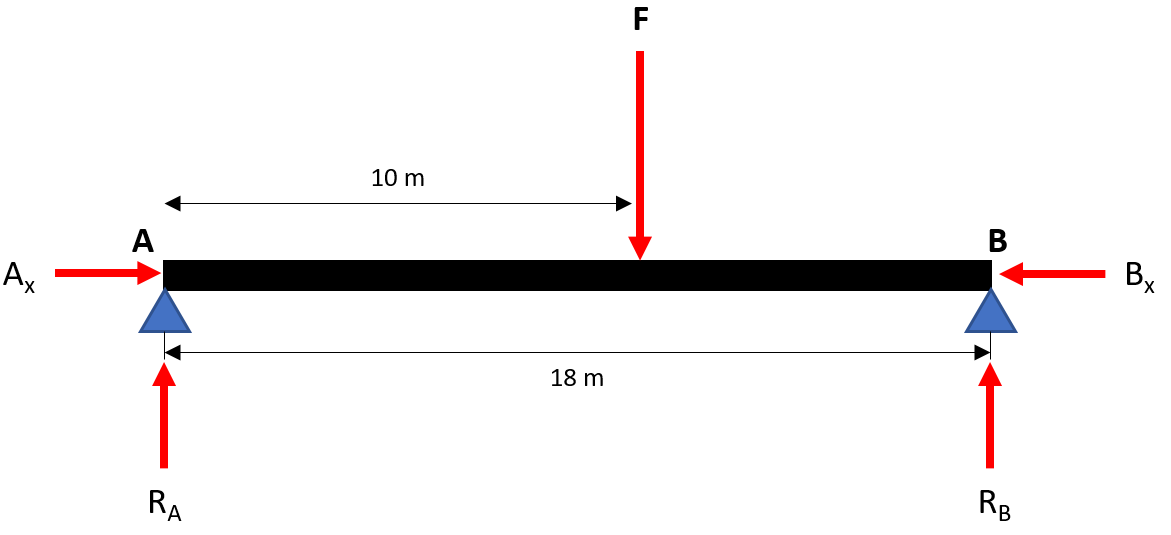
The triangular force distribution can be replaced with a concentrated force
$$F$$
, which is located through the triangle’s centroid. The force’s magnitude is equal to the triangle’s area:
$$$F=\frac{1}{2}bh=\frac{1}{2}(12m)(200N/m)=1,200\:N$$$
where
$$b$$
is the triangle’s base, and
$$h$$
is the triangle’s height.
We can take the moment about Point A to reduce our unknown variables down to 1 (
$$A_x$$
,
$$B_x$$
and
$$R_A$$
will zero out since their radius vector goes through Point A). Remember,
$$Moment=Force \times Distance$$
:
$$$\sum M_A=0=(18m)R_B-(10m)F$$$
$$$(18m)R_B=(10m)(1,200N)$$$
$$$R_B=\frac{(10m)(1,200N)}{18m}=\frac{12,000N}{18}=667\:N$$$
667 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Force
055. Free Body Diagram
164. Pulleys
193. Tensional Force
304. Vertical Force
310. Simply Supported
365. Beam AB
380. Reaction Point
449. Tire Swing
656. Beam
Similar Problems from FE Sub Section: Moment
304. Vertical Force
310. Simply Supported
365. Beam AB
380. Reaction Point
656. Beam
Similar Problems from FE Section: Force
055. Free Body Diagram
145. Force Characteristics
164. Pulleys
193. Tensional Force
304. Vertical Force
310. Simply Supported
365. Beam AB
380. Reaction Point
449. Tire Swing
656. Beam
Similar Problems from FE Section: Moments (Couples)
047. Stop at the Sign
304. Vertical Force
310. Simply Supported
365. Beam AB
380. Reaction Point
499. Torque Units
656. Beam