Reaction Point
Beam AB, which is simply supported at Points A & B, is subjected to a distributed load as shown. If the beam’s weight is negligible, what is the reaction force at Point A?
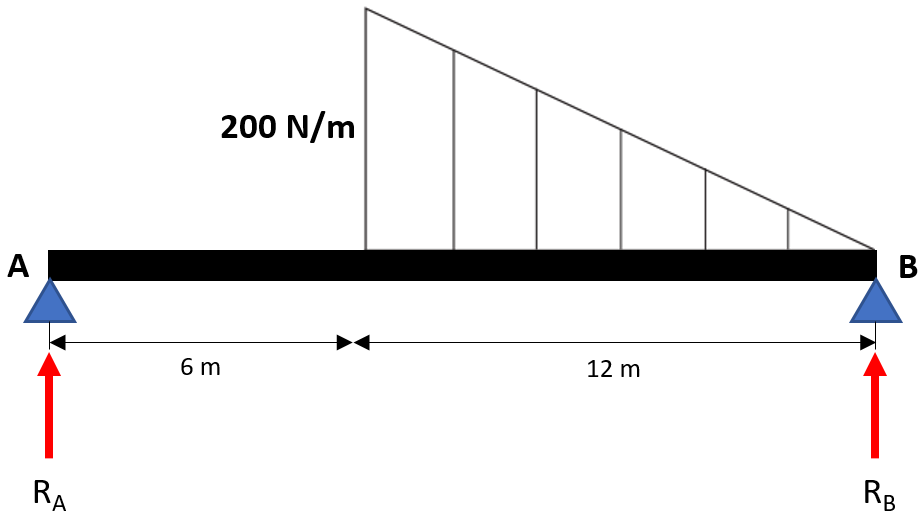
Expand Hint
Draw the free body diagram:
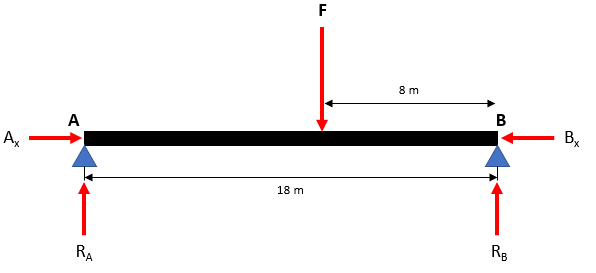
Hint 2
Take the moment about Point B to reduce the amount of unknown forces.
$$$\sum M_B=0=Force \times Distance$$$
First, draw the free body diagram:
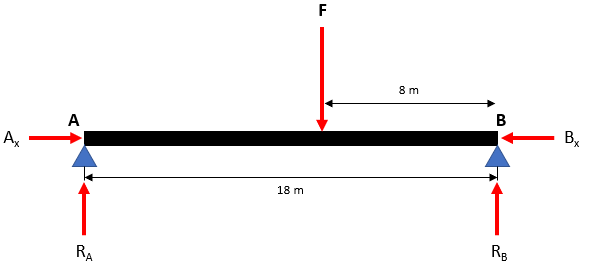
The triangular force distribution can be replaced with a concentrated force
$$F$$
, which is located through the triangle’s centroid. The force’s magnitude is equal to the triangle’s area:
$$$F=\frac{1}{2}bh=\frac{1}{2}(12m)(200N/m)=1,200\:N$$$
where
$$b$$
is the triangle’s base, and
$$h$$
is the triangle’s height.
We can take the moment about Point B to reduce our unknown variables down to 1 (
$$A_x$$
,
$$B_x$$
and
$$R_B$$
will zero out since their radius vector goes through Point B). Remember,
$$Moment=Force \times Distance$$
:
$$$\sum M_B=0=(18m)R_A-(8m)F$$$
$$$(18m)R_A=(8m)(1,200N)$$$
$$$R_A=\frac{(8m)(1,200N)}{18m}=\frac{9,600N}{18}=533.3\:N$$$
533.3 N
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Force
055. Free Body Diagram
164. Pulleys
193. Tensional Force
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
449. Tire Swing
656. Beam
Similar Problems from FE Sub Section: Moment
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
656. Beam
Similar Problems from FE Section: Force
055. Free Body Diagram
145. Force Characteristics
164. Pulleys
193. Tensional Force
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
449. Tire Swing
656. Beam
Similar Problems from FE Section: Moments (Couples)
047. Stop at the Sign
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
499. Torque Units
656. Beam
Similar Problems from FE Section: Systems of Forces
193. Tensional Force
449. Tire Swing