Tire Swing
Consider a tire swing found in a typical playground is suspended via 3 chain-link cables that experience a 90 N tensional force when a small child sits on the tire. If the angle formed between each cable and the tire is 65°, what is the child’s mass in kg? Ignore the weight of the tire and chain-link cables.

Expand Hint
The problem is asking to solve for
$$F_{y}$$
in the free body diagram:
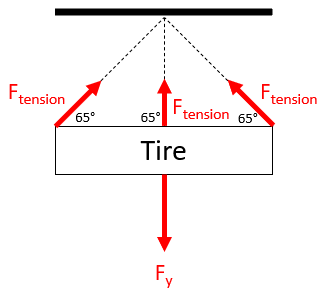
Hint 2
Newton’s 2nd law:
$$$F_y=mass\times acceleration$$$
The problem is asking to solve for
$$F_{y}$$
in the free body diagram:
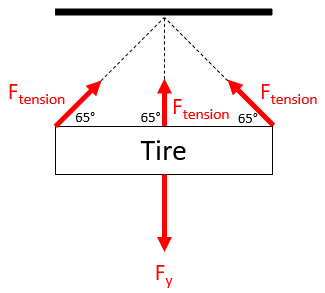
Because there are three upward pulling cables in the vertical direction, they will counteract the entire downward force. Keep in mind that
$$F_{tension}$$
has both a x-component and y-component, but only the vertical component is relevant to this situation. Thus:
$$$F_y=(3)F_{tension}\cdot sin(65^{\circ})=(3)(90N)\cdot sin(65^{\circ})=244.7\:N$$$
To find the child’s mass, recall Newton’s 2nd law:
$$$F_y=mass\times acceleration$$$
$$$mass=\frac{F_y}{gravity}=\frac{244.7N}{9.8\frac{m}{s^2}}=\frac{244.7kg\cdot \frac{m}{s^2}}{9.8\frac{m}{s^2}}=25\:kg$$$
25 kg
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Force
055. Free Body Diagram
164. Pulleys
193. Tensional Force
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
380. Reaction Point
656. Beam
Similar Problems from FE Section: Force
055. Free Body Diagram
145. Force Characteristics
164. Pulleys
193. Tensional Force
304. Vertical Force
310. Simply Supported
365. Beam AB
369. A Beam
380. Reaction Point
656. Beam
Similar Problems from FE Section: Systems of Forces
193. Tensional Force
380. Reaction Point