Inflections
For the curve represented by the equation below, find the point of inflection(s).
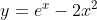
Expand Hint
First, find the second derivative of
$$f(x)$$
.
Hint 2
Set
$$f''(x)=0$$
to solve for the inflection point.
An inflection point is a point on the curve/graph at which concavity changes, and occurs when
$$f''(x)=0$$
.
Using the power rule for the first derivative and applying it twice, we’ll get the second derivative power rule:
$$$\frac{d^2}{dx^2}[x^n]=\frac{d}{dx}\frac{d}{dx}[x^n]=\frac{d}{dx}[nx^{n-1}]=n\frac{d}{dx}[x^{n-1}]=n(n-1)(x^{n-2})$$$
Thus, the second derivative is:
$$$f''(x)=e^x-2(2)(2-1)(x^{2-2})$$$
$$$=e^x-(4)(1)(x^{0})$$$
$$$f''(x)=e^x-(4)(1)(1)=e^x+4$$$
Note that
$$\frac{d(e^u)}{dx}=e^u\frac{du}{dx}$$
, which is why
$$e^x$$
remains unchanged after performing the second derivative. Solving for
$$x$$
when
$$f''(x)=0$$
to get the x-component inflection point:
$$$e^x-4=0$$$
$$$ln(e^x)=ln(4)$$$
$$$x=1.39$$$
The inflection point consists of both a
$$x$$
and
$$y$$
coordinate. We have solved the
$$x$$
component, but still need to determine the
$$y$$
component. To find
$$y$$
, plug the
$$x$$
component back into the original function:
$$$y=e^{1.39}-2(1.39)^2$$$
$$$y=4.01-2(1.93)=4.01-3.86=0.15$$$
Thus, the inflection point is at (1.39, 0.15)
(1.39, 0.15)
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: The Derivative
342. Inflection Point
355. Multi Roots
Similar Problems from FE Sub Section: Integral Calculus
040. Integrals
043. A Calc Question
044. Definite Integrals
077. Area Under a Curve
308. Definite Integral
408. Triple Integrals
416. Trip Integral
430. A Curve’s Area
643. Integral Finding
Similar Problems from FE Section: Differential Calculus
040. Integrals
043. A Calc Question
044. Definite Integrals
048. Derivative
051. 2nd Derivatives
077. Area Under a Curve
078. Derivatives
122. Roller Coasters
158. A Train's Velocity
308. Definite Integral
312. The Derivative
342. Inflection Point
355. Multi Roots
394. Acceleration
408. Triple Integrals
412. Hill Bomb
416. Trip Integral
430. A Curve’s Area
643. Integral Finding
650. Differentiate