Critical Crack Length
Consider a part is formed by bending a sheet of 4340 Steel, which has a Fracture Toughness of 46 MPa∙m^(1/2), and a yield strength of 470 MPa. What is the max crack length that can be tolerated for an exterior crack in mm?
Expand Hint
$$$K_{IC}=Y\cdot \sigma \cdot \sqrt{\pi (a)}$$$
where
$$K_{IC}$$
is fracture toughness,
$$\sigma$$
is applied stress,
$$a$$
is crack length, and
$$Y$$
is geometrical factor.
Hint 2
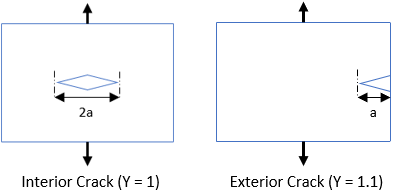
Fracture toughness is the stress intensity of when a brittle material will fail due to the combination of an applied stress and crack length.
$$$K_{IC}=Y\cdot \sigma \cdot \sqrt{\pi (a)}$$$
where
$$K_{IC}$$
is fracture toughness,
$$\sigma$$
is applied stress,
$$a$$
is crack length, and
$$Y$$
is geometrical factor.
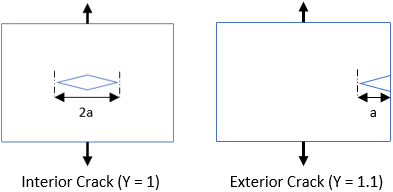
Based on the problem statement:
- $$\sigma=470\:MPa$$
- $$Y=1.1$$ (since an exterior crack will be produced)
- $$K_{IC}=46\:MPa\cdot m^{1/2}$$
Solving for crack length:
$$$a=\left (\frac{K_{IC}}{Y\cdot \sigma} \right )^2\cdot \frac{1}{\pi}$$$
$$$a=\left (\frac{46MPa\cdot \sqrt{m}}{(1.1)(470MPa)} \right )^2\cdot \frac{1}{\pi}=\frac{0.0079m}{\pi }=0.0025=2.5\:mm$$$
2.5 mm
Time Analysis
See how quickly you looked at the hint, solution, and answer. This is important for making sure you will finish the FE Exam in time.- Hint: Not clicked
- Solution: Not clicked
- Answer: Not clicked
Similar Problems from FE Sub Section: Mechanical
004. Stress and Strain
007. Aluminum Alloy Graphs
076. Stress vs Strain Curves
167. Material Crack
172. Tensile Test
315. Composite Material
319. Composite Strain
349. Compressibility Modulus
354. Yield vs Ultimate Strength
358. Brittle vs Ductile vs Plastic
407. Composite Modulus
445. Fracture Toughness
455. Fracture Stress
495. Yield and Ultimate Strength
538. Fracture
636. Base Material
653. Goodman vs Soderberg
Similar Problems from FE Section: Properties of Materials
004. Stress and Strain
007. Aluminum Alloy Graphs
076. Stress vs Strain Curves
167. Material Crack
172. Tensile Test
315. Composite Material
319. Composite Strain
349. Compressibility Modulus
354. Yield vs Ultimate Strength
358. Brittle vs Ductile vs Plastic
407. Composite Modulus
445. Fracture Toughness
455. Fracture Stress
495. Yield and Ultimate Strength
538. Fracture
542. Resistivity
544. Conductivity
636. Base Material
653. Goodman vs Soderberg